本文共 2753 字,大约阅读时间需要 9 分钟。
前一部分中,我们介绍了如何在Python和Theano框架下实现RNN,但还未深入了解时序反向传播算法(BPTT)是如何计算梯度的。
这周,我们将简单介绍BPTT,并解释其与传统反向传播的区别。我们还将了解梯度消失问题,这也是推动LSTM(长短时记忆)和GRU(门控循环单元)(目前在NLP和其他领域最流行且有效模型)发展的原因。1991年,梯度消失问题最早由Sepp Hochreiter发现,又因深度框架的广泛应用再次受到关注。以下是本系列教程的四个部分:1.循环神经网络(RNN)的基本介绍2.在Python和Theano框架下实现RNN3.基于时间的反向传播算法(BPTT)和梯度消失问题(本部分)4.建立基于门控循环单元(GRU)或者长短时记忆(LSTM)的RNN模型
说明:为完全掌握本部分教程,建议您对偏微分(也称偏导数)和基本反向传播的工作原理有所了解,以下是三篇关于反向传播算法的教程供大家参考:
http://cs231n.github.io/optimization-2/http://colah.github.io/posts/2015-08-Backprop/http://neuralnetworksanddeeplearning.com/chap2.html-1-时序反向传播算法 (BPTT)
先来快速回忆一下RNN的基本方程。注意,为了和要引用的文献保持一致,这里我们把o改成了![]() 。
。
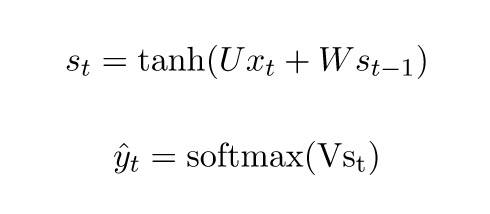 同样,将损失函数定义为交叉熵损失函数,如下所示:
同样,将损失函数定义为交叉熵损失函数,如下所示:
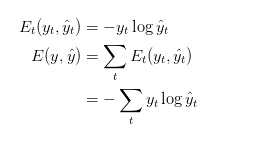
在这里,y_t是表示的是时间步t上的正确标签,![]() 是我们的预测。通常我们会将一个完整的句子序列视作一个训练样本,因此总误差即为各时间步(单词)的误差之和。
是我们的预测。通常我们会将一个完整的句子序列视作一个训练样本,因此总误差即为各时间步(单词)的误差之和。
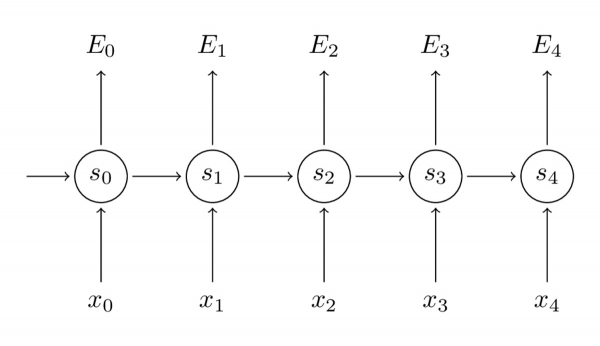
▲RNN反向传播
别忘了,我们的目的是要计算误差对应的参数U、V和W的梯度,然后借助SDG算法来更新参数。当然,我们统计的不只是误差,还包括训练样本在每时间步的梯度:
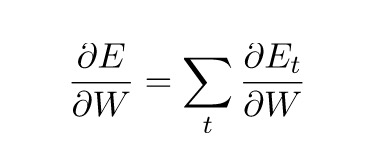
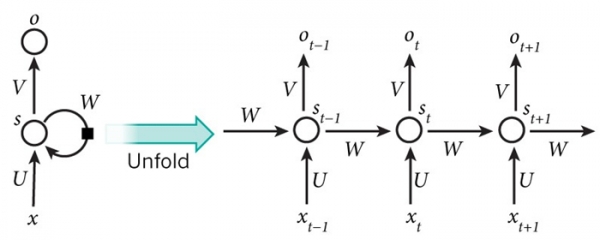
▲RNN的结构图
我们借助导数的链式法则来计算梯度。从最后一层将误差向前传播的思想,即为反向传播。本文后续部分将以E3为例继续介绍:
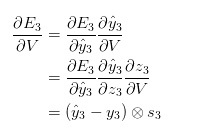
由上可知,z_3 =Vs_3,![]() 为两个矢量的外积。为了让大家更好理解,这里我省略了几个步骤,你可以试着自己计算这些导数。我想强调的是,
为两个矢量的外积。为了让大家更好理解,这里我省略了几个步骤,你可以试着自己计算这些导数。我想强调的是,![]() 的值仅取决于当前时间步的值:
的值仅取决于当前时间步的值:![]() 。有了这些值,计算参数V的梯度就是简单的矩阵相乘了。
。有了这些值,计算参数V的梯度就是简单的矩阵相乘了。
但![]() 有所不同。我们列出如前文所示的链式法则来解释原因:
有所不同。我们列出如前文所示的链式法则来解释原因:
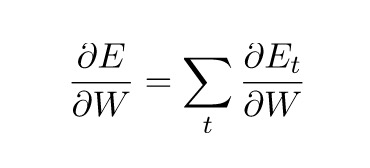
▲链式求导式子1
其中,s_3 = tanh(Ux_t + Ws_2) 取决于s_2,而s_2则取决于W和s_1,以此类推。因此,如果要推导参数W,就不能简单将s_2视作常量,需要再次应用链式法则,真正得到的是:
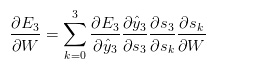
▲链式求导式子2
上面的式子用到了复合函数的链式求导法则,将每个时间步长对梯度的贡献相加。换言之,由于参数W时间步长应用于想要的输出,因此需从t=3开始通过所有网络路径到t=0进行反向传播梯度:
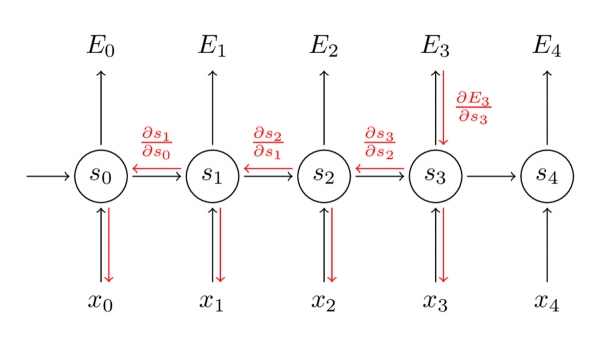
▲BPTT复合函数链式求导
5个时间步梯度的递归神经网络展开图 请注意,这与我们在深度神经网络中应用的标准反向传播算法完全一致。主要区别在于我们对每时间步的参数W的梯度进行了求和。传统的神经网络(RNN)中,我们不在层与层之间共享参数,也就无需求和。但就我而言,BPTT不过是标准反向传播在展开RNN上的别称。好比在反向传播算法中,可以定义一个反向传播的delta矢量,例如:基于z_2 = Ux_2+ Ws_1的 。和传统的反向传播算法一样,我们仍然可以定义残差,然后计算梯度。
。和传统的反向传播算法一样,我们仍然可以定义残差,然后计算梯度。
直接实现BPTT的代码如下:

该代码解释了难以训练RNN的原因:因为序列(句子)很长,可能由20个或以上单词组成,因此需反向传播多层网络。在实际操作时,许多人会在反向传播数步后进行截断成比较长的步骤,正如上面代码中的bptt_truncate参数定义的那样。
-2-梯度消失问题
本教程的前面章节提到过RNN中,相隔数步的单词间难以形成长期依赖的问题。而英文句子的句意通常取决于相隔较远的单词,例如“The man who wore a wig on his head went inside”的语意重心在于一个人走进屋里,而非男人戴着假发。但普通的RNN难以捕获此类信息。那么不妨通过分析上面计算出的梯度来一探究竟:

别忘了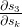 本身为链式法则!例如,
本身为链式法则!例如, 。还要注意,我们在对向量函数的向量求导,结果是一个矩阵(名为雅可比矩阵),所有元素均为逐点的导数。因此,上述梯度可重写为:
。还要注意,我们在对向量函数的向量求导,结果是一个矩阵(名为雅可比矩阵),所有元素均为逐点的导数。因此,上述梯度可重写为:

然而,上述雅克比矩阵中2范数(可视为绝对值)的上限是1(此处不做证明)。直观上,tanh激活函数将所有的值映射到-1到1这个区间,导数值也小于等于1(sigmoi函数的导数值小于等于1/4):
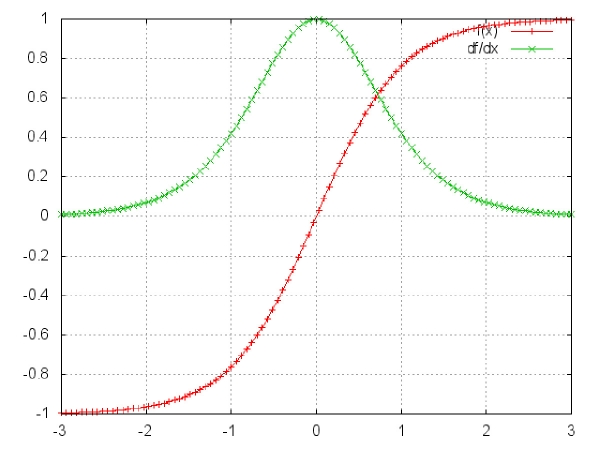
▲tanh及其导数。图片源自:http://nn.readthedocs.org/en/rtd/transfer/
可以看到tanh和sigmoid函数在两端的导数均为0,近乎呈直线状(导数为0,函数图像为直线),此种情况下可称相应的神经元已经饱和。两函数的梯度为0,使前层的其它梯度也趋近于0。由于矩阵元素数值较小,且矩阵相乘数次(t - k次)后,梯度值迅速以指数形式收缩(意思相近于,小数相乘,数值收缩,越来越小),最终在几个时间步长后完全消失。“较远”的时间步长贡献的梯度变为0,这些时间段的状态不会对你的学习有所贡献:你最终还是无法学习长期依赖。梯度消失不仅存在于循环神经网络,也出现在深度前馈神经网络中。区别在于,循环神经网络非常深(本例中,深度与句长相同),因此梯度消失问题更为常见。
不难想象,如果雅克比矩阵的值非常大,参照激活函数及网络参数可能会出现梯度爆炸,即所谓的梯度爆炸问题。相较于梯度爆炸,梯度消失问题更受关注,主要有两个原因:其一,梯度爆炸现象明显,梯度会变成Nan(而并非数字),并出现程序崩溃;其二,在预定义阈值处将梯度截断(详情请见本文章)是一种解决梯度爆炸问题简单有效的方法。而梯度消失问题更为复杂,因为其现象不明显,且解决方案尚不明确。
幸运的是,目前有一些方法可解决梯度消失问题。合理初始化矩阵 W可缓解梯度消失现象。还可采用正则化方法。此外,更好的方法是使用 ReLU,而非tanh或sigmoid激活函数。ReLU函数的导数是个常量,0或1,因此不太可能出现梯度消失现象。
更常用的方法是借助LSTM或GRU架构。1997年,首次提出LSTM ,目前该模型在NLP领域的应用极其广泛。GRU则于2014年问世,是LSTM的简化版。这些循环神经网络旨在解决梯度消失和有效学习长期依赖问题。相关介绍请见本教程下一部分。